 Herhangi bir alıntının sol tarafındaki Amazon logosunun üzerine tıkladığınızda ve Amazon.com’ dan kitap (veya diğer medya) satın alırsanız, MIT Açık Ders Malzemeleri bu satın alımınızdan ve yaptığınız diğer alımlardan %10 kazanacaktır. Bu satın alma maliyetinin artacağı anlamına gelmemektedir. Linkler ABD Amazon sitesine sağlanmıştır, ancak diğer bölgelerden de Amazon siteleri vasıtasıyla ADM’ yi destekleyebilirsiniz. Daha fazla bilgi edinin. Herhangi bir alıntının sol tarafındaki Amazon logosunun üzerine tıkladığınızda ve Amazon.com’ dan kitap (veya diğer medya) satın alırsanız, MIT Açık Ders Malzemeleri bu satın alımınızdan ve yaptığınız diğer alımlardan %10 kazanacaktır. Bu satın alma maliyetinin artacağı anlamına gelmemektedir. Linkler ABD Amazon sitesine sağlanmıştır, ancak diğer bölgelerden de Amazon siteleri vasıtasıyla ADM’ yi destekleyebilirsiniz. Daha fazla bilgi edinin. |
Haftalık Ders SaatleriDersler: 2 kez / hafta, 1.5 saat / ders
Dersin AmacıBu dersin amacı, analitik fonksiyonlar teorisinin yöntemlerini ve esas tekniklerini öğretmektir. Bu notlar reel analizden oldukça farklı olup biraz daha fazla geometrik vurguya sahiptir. Ayrıca analitik sayılar kuramı gibi diğer alanlara da önemli uygulamaları vardır.
ÖnkoşulAnaliz I (18.100B) veya dengi.
Ders Kitabı Ahlfors, Lars V. Complex Analysis: An Introduction to the Theory of Analytic Functions of One Complex Variable. 3rd ed. New York, NY: McGraw-Hill, 1979. ISBN: 9780070006577.
Ahlfors, Lars V. Complex Analysis: An Introduction to the Theory of Analytic Functions of One Complex Variable. 3rd ed. New York, NY: McGraw-Hill, 1979. ISBN: 9780070006577.
Bu ders kitabı, geometrik havası olan ilgi çekici bir kitaptır. Bu ders, 232. sayfaya kadar olan konuların çoğunu kapsayacak fakat, kitaptaki Riemann zeta fonksiyonu ile doğal olarak oldukça ilgili olan, Asal Sayı Teoreminin tam ispatına ayrılmış iki ders eklenecektir.
Derslerin birçoğunda kitapta olmayan, kısmen değişik ispatlarla, bazı konular verilecek ve kısmen biraz daha ilginç soruların çözümleri ile çalışılacaktır. Ders #2, 13, 14, 16, 19, 21 ve 22 deki işleyiş kitapta bu konulara karşı gelen notlardan gerçekten oldukça farklıdır. Ders #21 ve 22 aslında Asal Sayı Teoreminin tam ispatını içerir.
Dersler kitaptaki biçiminden oldukça ayrıldığı için, derslere düzenli katılımı şiddetle tavsiye ederim.
ÖdevlerHer Perşembe günü verilecek ve sonraki Perşembe toplanacaktır. Ödevler ders kitabındaki problemler arasından seçilecektir.
Sınavlar4. ve 16. derslerden sonra sınıfta 2 test uygulanacaktır. Bunlara ek olarak bir final sınavı yapılacaktır.
PuanlamaFinal notu birikimli puan üzerinden hesaplanacaktır.
| ETKİNLİKLER | YÜZDELERİ |
|---|
| Ödevler | 10% |
| İki sınıf içi testi (her biri 20%) | 40% |
| Final sınavı | 50% |
Ödev problemlerle uğraşmak konuyu anlamanız ve öğrenmeniz için çok önemlidir. Bunun için oldukça fazla zamanınız olduğunu unutmayınız. Arkadaşlarınızla problemlerin çözümü üzerine tartışmanız sizin için yararlı olacaktır, ancak çözümleri kendi açıklamalarınızla yapmanız gerekmektedir. Bu süreç, sizin daha iyi bir çözüm bulmanıza yardımcı olacaktır. Çözümlerinizi özenle sunmanız sizin için oldukça önemlidir. Bu sizin matematiksel yazım sitilinizi geliştirmeniz için en uygun yerdir. (Tex yazılımı en çok rağbet görendir). Dikkatsizce ve özensizce yapılmış ödevler kabul edilmeyecektir.
Kompleks değişkenli fonksiyonlar teorisi üzerine yayımlanmış birçok kitap mevcuttur. Bunların bazılarını kütüphanede taramanızı tavsiye ederim. Örneğin, Caratheódory’ nin Fonksiyonlar Teorisi cilt I ve II bizim kitabımıza oldukça yakındır. Buna ek olarak, özellikle Pólya and Szegö’ nin yazdığı Analizde Teoremler ve Problemler isimli kitabın birçok bölümü kompleks değişkenler konusu üzerinedir. Rudin’in Reel ve Kompleks Analiz isimli kitabı da oldukça önemli kaynakçadır.
 Caratheódory, Constantin. Theory of Functions of a Complex Variable. Rhode Island: AMS Chelsea Pub, 2001. ISBN: 9780821828311.
Caratheódory, Constantin. Theory of Functions of a Complex Variable. Rhode Island: AMS Chelsea Pub, 2001. ISBN: 9780821828311.
Caratheódory, Constantin, and F. Steinhardt. Theory of Functions of a Complex Variable. Vol. 2. New York, NY: Chelsea, 1960.
 Pólya, George, and Gábor Szego. Problems and Theorems in Analysis. Berlin: Springer, 1978. ISBN: 9780387056722.
Pólya, George, and Gábor Szego. Problems and Theorems in Analysis. Berlin: Springer, 1978. ISBN: 9780387056722.
 Rudin, Walter. Real and Complex Analysis. New York, NY: McGraw-Hill, 1986. ISBN: 9780070542341.
Rudin, Walter. Real and Complex Analysis. New York, NY: McGraw-Hill, 1986. ISBN: 9780070542341.
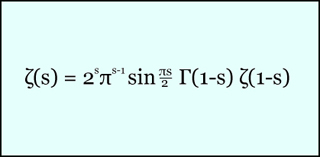
 Herhangi bir alıntının sol tarafındaki Amazon logosunun üzerine tıkladığınızda ve Amazon.com’ dan kitap (veya diğer medya) satın alırsanız, MIT Açık Ders Malzemeleri bu satın alımınızdan ve yaptığınız diğer alımlardan %10 kazanacaktır. Bu satın alma maliyetinin artacağı anlamına gelmemektedir. Linkler ABD Amazon sitesine sağlanmıştır, ancak diğer bölgelerden de Amazon siteleri vasıtasıyla ADM’ yi destekleyebilirsiniz.
Herhangi bir alıntının sol tarafındaki Amazon logosunun üzerine tıkladığınızda ve Amazon.com’ dan kitap (veya diğer medya) satın alırsanız, MIT Açık Ders Malzemeleri bu satın alımınızdan ve yaptığınız diğer alımlardan %10 kazanacaktır. Bu satın alma maliyetinin artacağı anlamına gelmemektedir. Linkler ABD Amazon sitesine sağlanmıştır, ancak diğer bölgelerden de Amazon siteleri vasıtasıyla ADM’ yi destekleyebilirsiniz.