Fareniz x vektörünün hareket etmesini sağlar. Aynı zamanda grafik de
Ax’i renkli ve hareketli olarak gösterir. Görünen yeşil daire birim
çember olup, kırmızı oval ise onun matris etkisi altındaki görüntüsüdür.
x vektörünü değiştirdiğinizde onlar da değişir.
Ax’in x’in önünde veya arkasında olması mümkündür. Bazen de Ax
x’e paralel olur. Bu paralellik anında, Ax=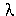 x
olup, x bir özvektör olur. x
olup, x bir özvektör olur.
Bu 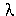 özdeğeri Ax in doğrultusundan ve
uzunluğundan gelir. A matrisinin seçimine bağlı olarak, Applet çeşitli
olasılıkları gösterecektir. özdeğeri Ax in doğrultusundan ve
uzunluğundan gelir. A matrisinin seçimine bağlı olarak, Applet çeşitli
olasılıkları gösterecektir.
1. Gerçel özvektörler yok. x ve Ax asla aynı doğrultuda olmaz.
Özdeğerler ve özvektörler karmaşık sayılardır.
2. Tek bir özvektör doğrusu var. x ve Ax doğrultuları
hareket ederken karşılaşabilir, ama biri diğerini geçemez.
3. Özvektörlerin iki bağımsız doğrultusu var. Bu normal! Ax
ile x birinci özvektörde ve sonra da ikinci özvektörde kesişir.
A’nın tekil (rankı bir) bir matris olduğunu varsayalım. Onun sütun uzayı bir
doğrudur. Ax vektörü bu doğru üzerinde hareket etmek zorunda, sağa sola
hareket edemez.
x özvektörünün biri bu doğru boyunca olur. Diğer özvektör, Ax
= 0 olduğunda gözükür. Sıfır, tekil bir matrisin bir özdeğerdir.
Aşağıdaki matrisler için x ve Ax’i izleyebilirsiniz. Kaç tane
özvektörü var ve nerede? Ax saattin ters yönü yerine saat yönün de ne
zaman gider?
A=([0, -1], [1, 0])
A=([3, 0], [0, 3])
A=([1, 3], [1, 0]) (kusurlu)
A=([1, 2], [2, 1])
|